Vulnerability, Exposure, and Impacts
Lecture
Mon., Jan. 22
Today
Given some hazard, how do we assess the damages or impacts?
We can quantify this, for example as \[ \textrm{Damage} = \textrm{Vulnerability} \times \textrm{Exposure} \times \textrm{Hazard} \]
Let’s understand these terms through some examples!
Illustrative examples
Today
Illustrative examples
How to manage exposure and vulnerability?
Some math
Wrapup
Structural fragility curve
\[ \Pr(\textrm{failure}) = f(\textrm{hazard}, \theta) \]
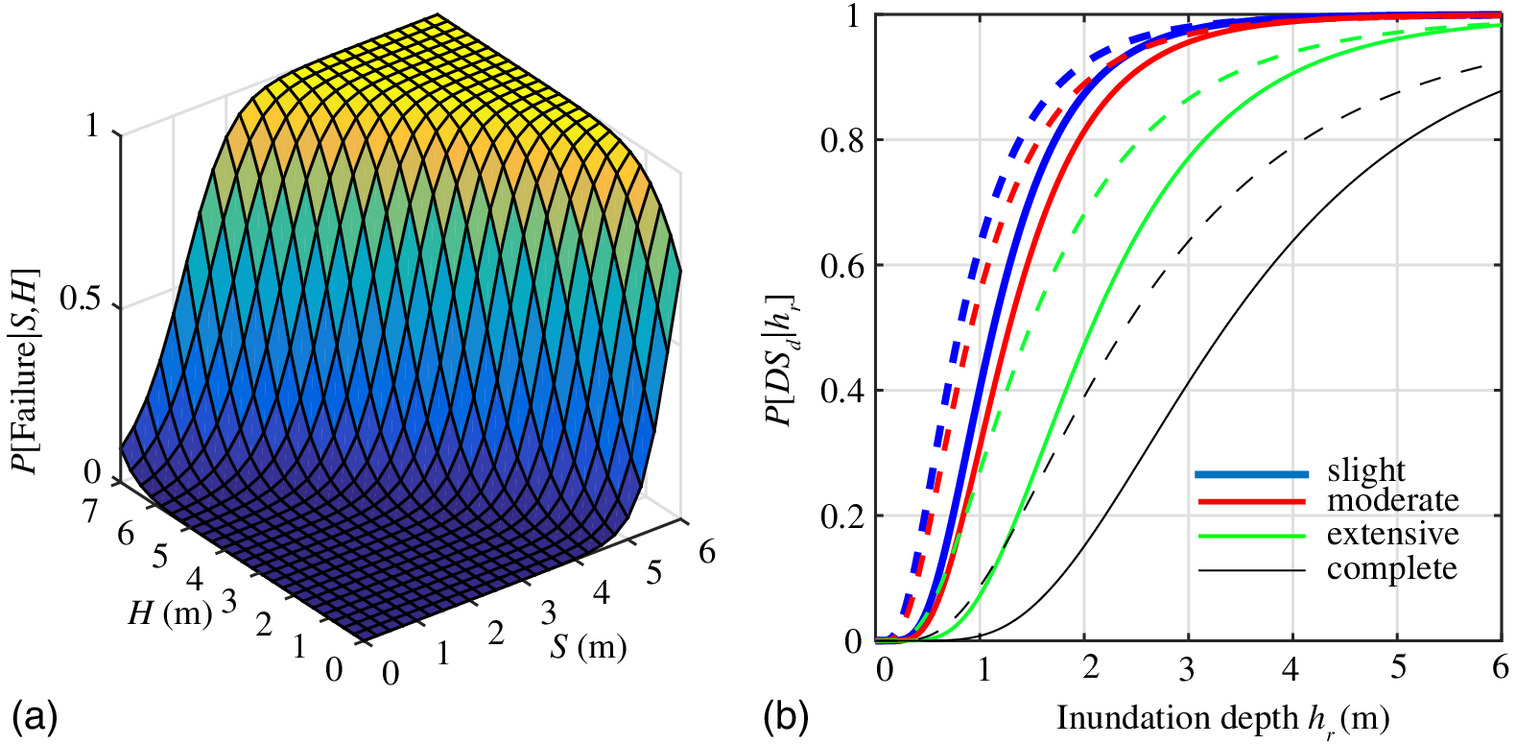
Figure 1: Parameterized fragilities as a function of surge and wave height for MSSS concrete bridges in South Carolina (a). (b): fragility curves for bridges subjected to tsunami hazard for low (solid lines) and moderate (dashed lines) flow rates (Gidaris et al., 2017).
Flood depth-damage curve
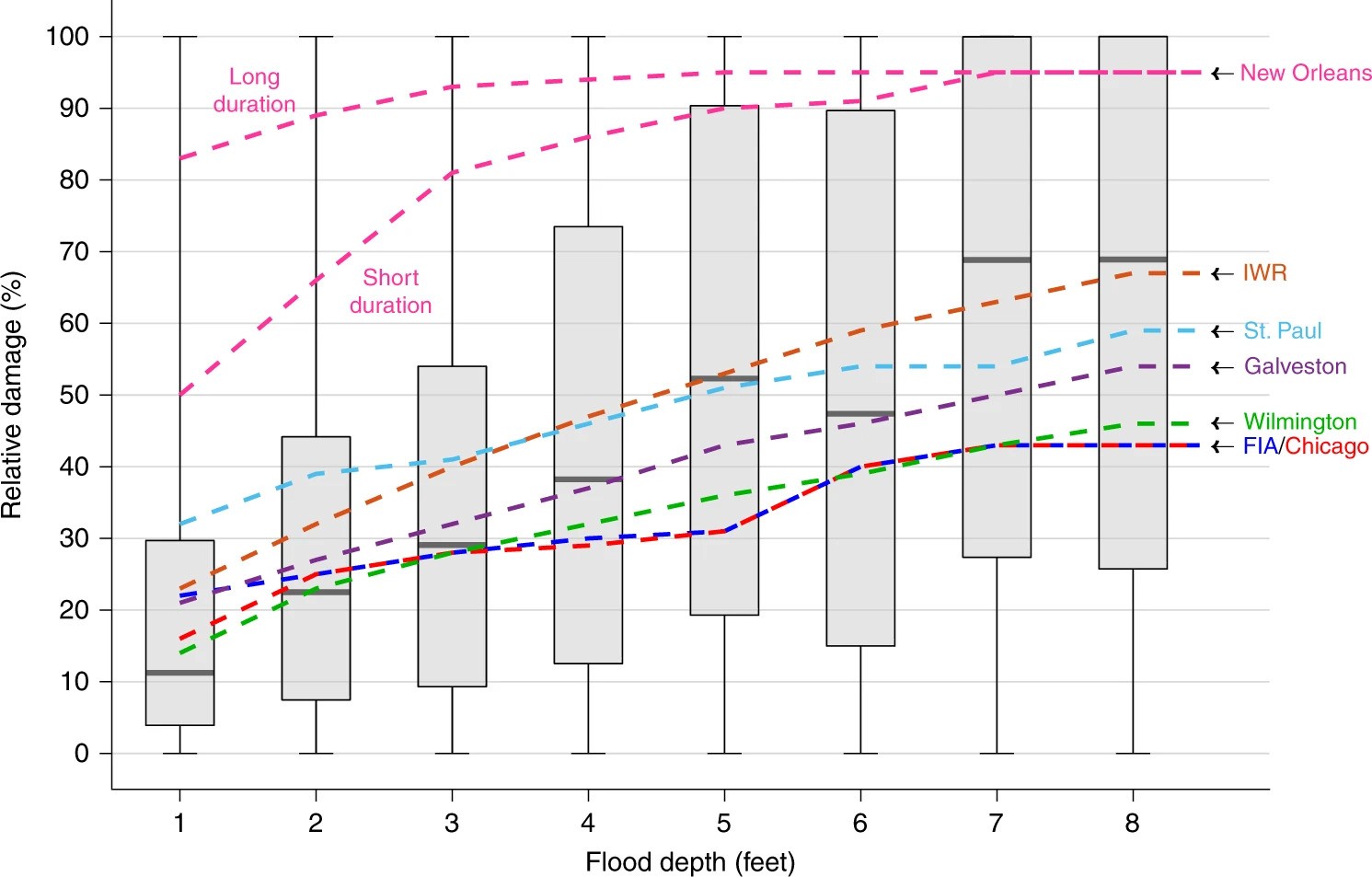
Figure 2: Boxplots show Wing et al. (2020) analysis of insurance claims. Lines show USACE depth-damage curves.
Seawall cost-benefit analysis
For a given storm, the total damages can be estimated by summing the damages for each property. \[ \textrm{Total damages} = \sum_{i \in \, \textrm{exposure}} \textrm{Hazard}_i \times \textrm{Vulnerability}_i \]
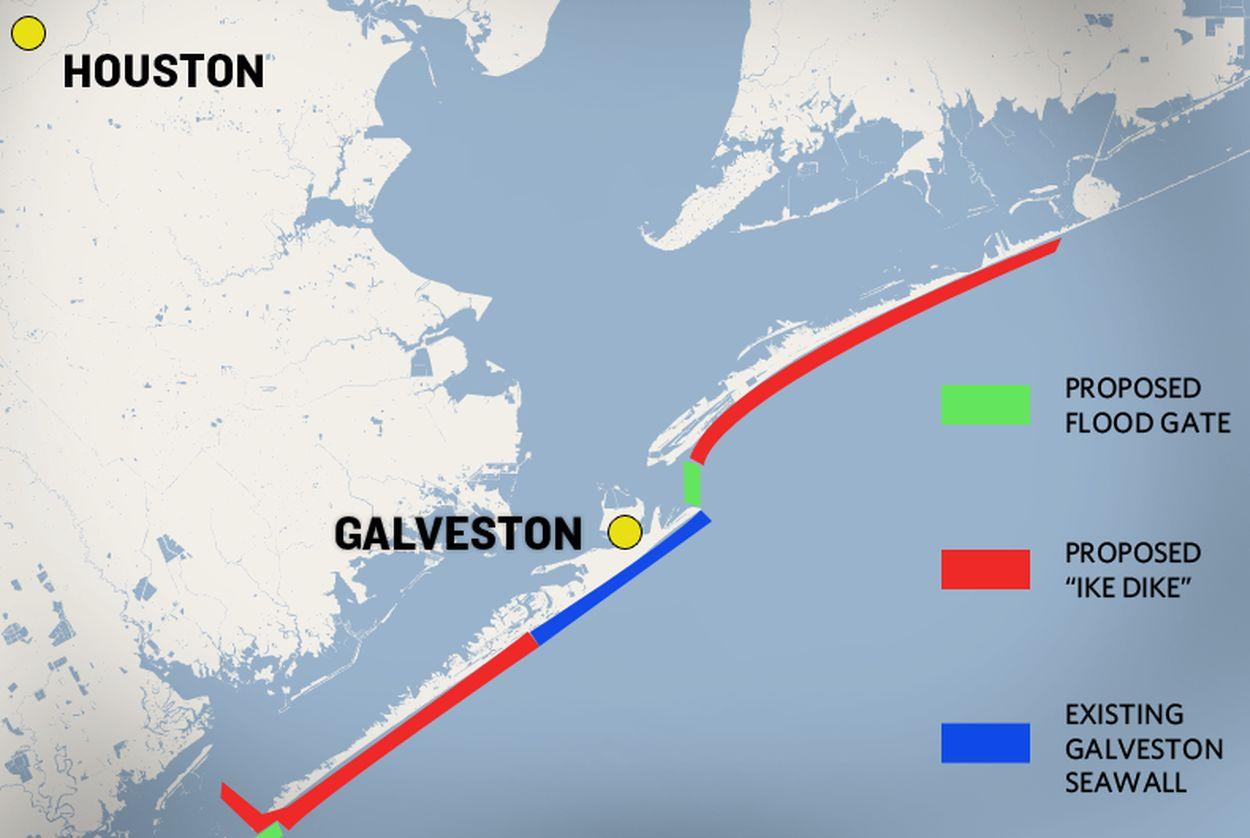
Figure 3: Proposed “Ike Dike”
Insurance portfolio risk
This is the most straightforward example of the exposure-vulnerability-hazard framework
- Hazard: a real or synthetic storm
- Exposure: all the assets that are insured
- Vulnerability: predicted losses as a function of the hazard
How to manage exposure and vulnerability?
Today
Illustrative examples
How to manage exposure and vulnerability?
Some math
Wrapup
Trends in exposure
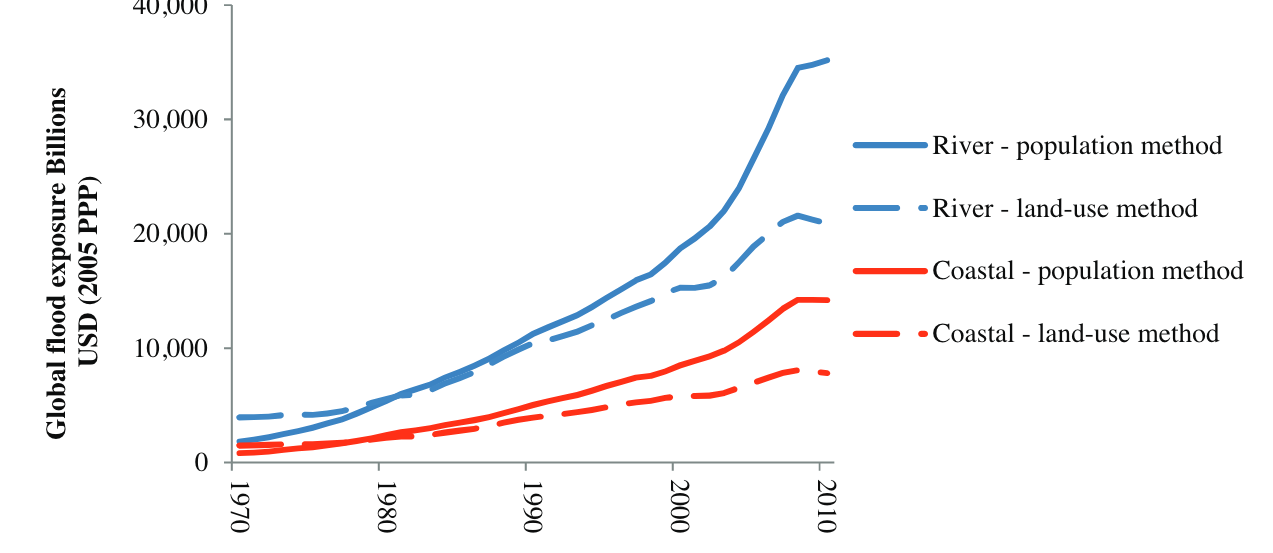
Figure 4: Global asset exposure to river and coastal flooding using the population and land-use methods (Jongman et al., 2012).
Example: North Carolina
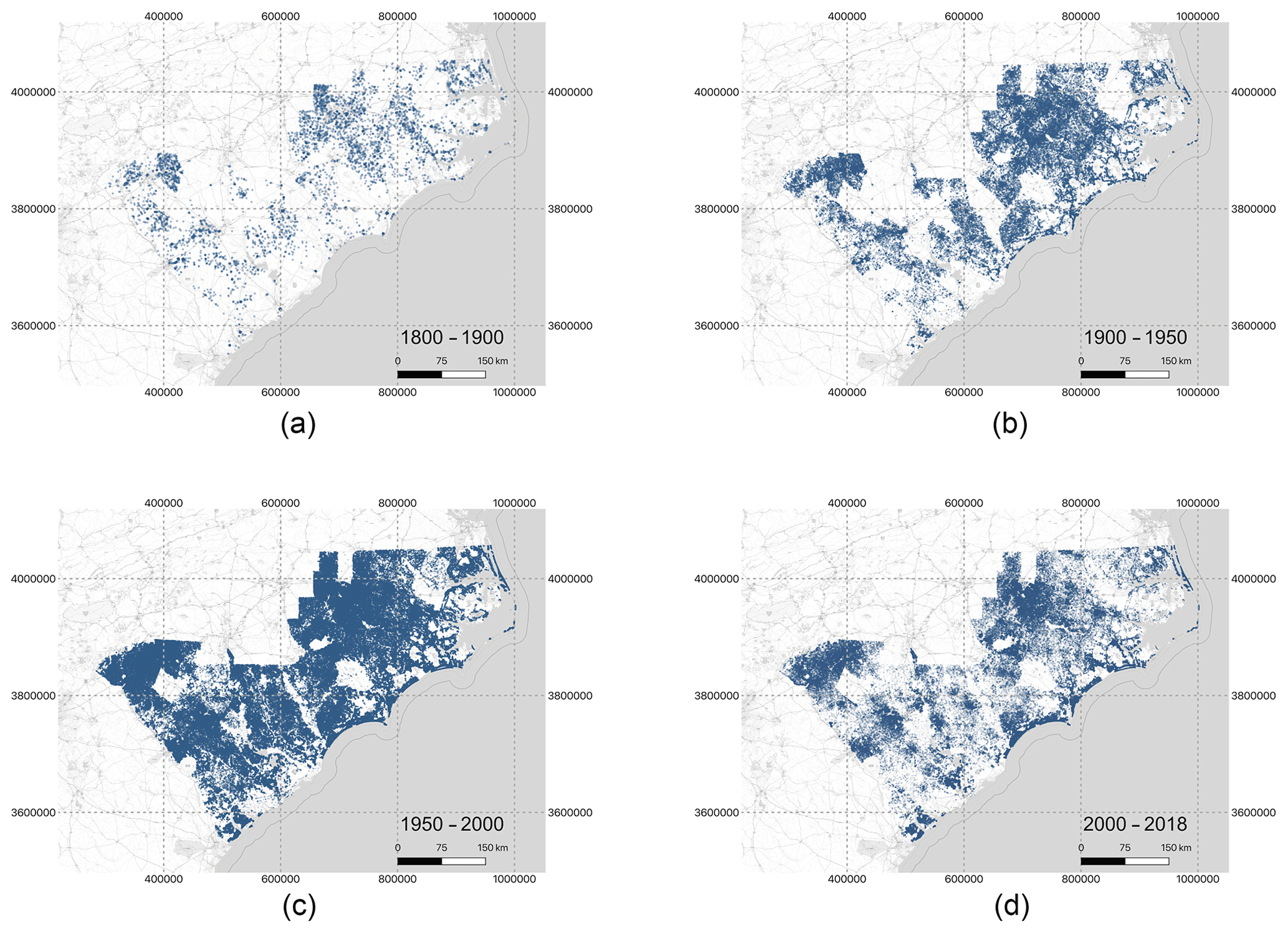
Figure 5: Spatial distribution of the properties within our database that were built during the (a) 1800–1900, (b) 1900–1950, (c) 1950–2000 and (d) 2000–2018 periods (Tedesco et al., 2020).
Changing vulnerability
Interventions such as floodproofing can shift the vulnerability curve

Figure 6: Floodproofing in Houston, TX (Houston Public Media)
Some math
Today
Illustrative examples
How to manage exposure and vulnerability?
Some math
Wrapup
Expectation
The expected value of a function \(f(x)\) of a random variable \(x\) is: \[ \mathbb{E}[f(x)] = \int f(x) p(x) dx \] where \(p(x)\) is the probability density function of \(x\).
In other words, for each possible value of \(x\), calculate \(f(x)\). We then take a weighted average, where the weights are the probability of each value of \(x\).
Key insight
You cannot get the expected value of a function by plugging the expected value of the random variable into the function. \[ \mathbb{E}[f(x)] \neq f(\mathbb{E}[x]) \]
Expected damages
If we want to calculate the expected damages then we can use this formula \[ \mathbb{E}[f(x)] = \int f(x) p(x) dx \] by defining \(x\) to be the hazard (e.g., flood depth) and \(f(x)\) the damage function.
Important
The key assumption we need is that we know the probability density function \(p(x)\)!
Monte Carlo approximation
In general, \(\int f(x) p(x) dx\) is hard to compute analytically. We can use Monte Carlo methods to approximate this integral.
Important
Monte Carlo methods are a wide class of computational algorithms for approximating integrals.
Monte Carlo expectation
If we draw \(N\) samples independently and identically distributed (i.i.d.) from a probability distribution \(p(x)\), denoted as \(\left\{x_i\right\}_{i=1}^N\) where \(x_i \sim p(x)\), then \[ \mathbb{E}[f(x)] \approx \frac{1}{N} \sum_{i=1}^N f(x_i) \]
Tip
Drawing \(N\) samples iid from \(p(x)\) can be inefficient. Most of the samples will be in regions where \(f(x)\) is small, so we are wasting computational effort. There are many clever ways around this.
For example: Trapezoidal EAD
Running regional flood models is computationally expensive. Often, a model may have been run for a few different nominal return levels. For example, we might have flood depths at each grid for the nominal 10, 25, 50, 100, 250, and 500 year floods.
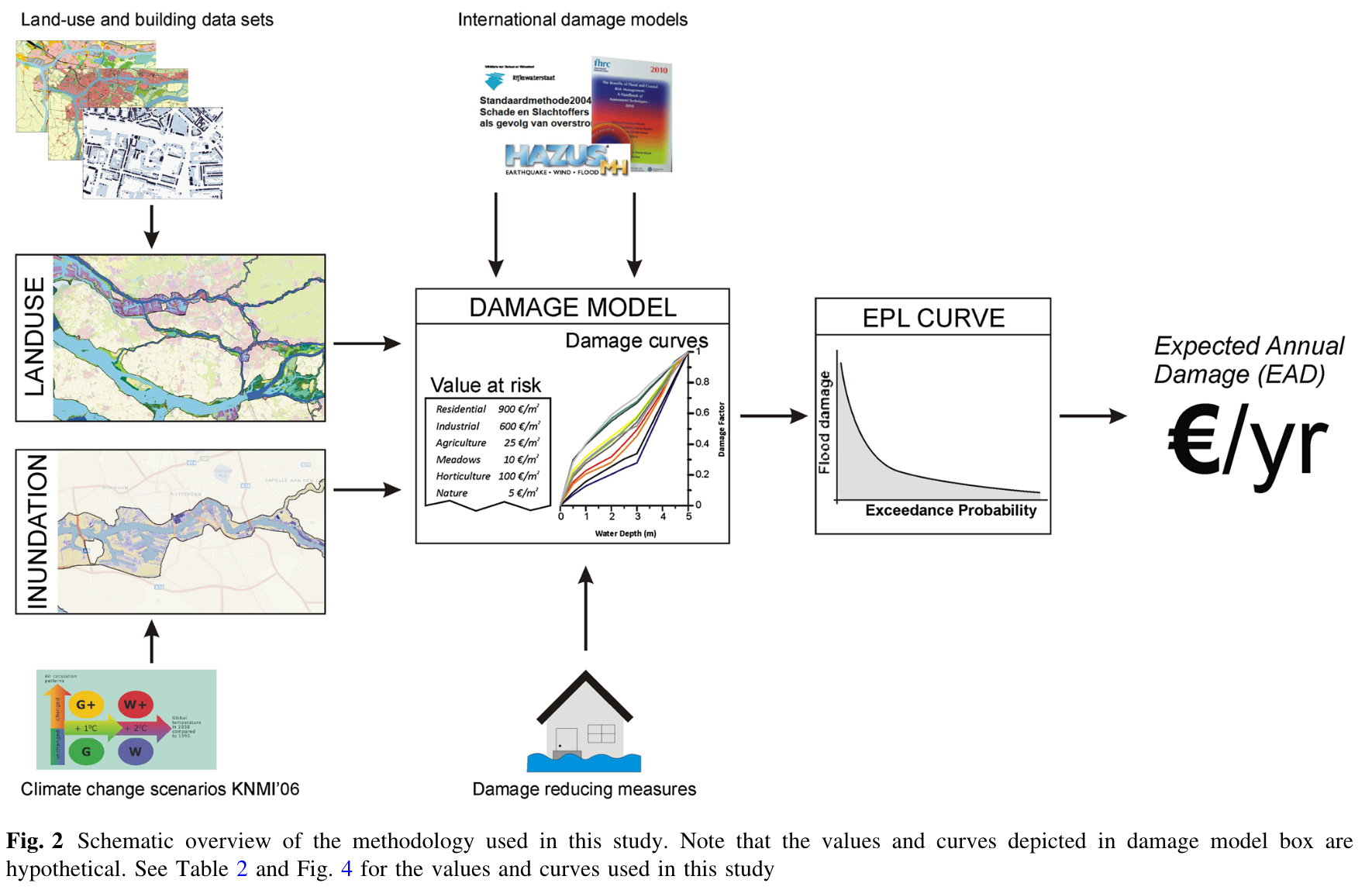
Wrapup
Today
Illustrative examples
How to manage exposure and vulnerability?
Some math
Wrapup
Key points
- Impacts (damage) depend on hazard, exposure, and vulnerability.
- Exposure and vulnerability are changing rapidly.
- To estimate risk, we need a model for how our system responds to a hazard.
- If we know the probability density function of the hazard, we can use Monte Carlo methods to estimate expected impacts.
Limitations of this framework
- How to think about damages that are not direct damages (e.g., “indirect” damages)?
- How to think about complex systems and risks (e.g., breadbasket failures) that are not easy summarized by a single metric?
Logistics
- Wednesday: discussion questions for Wing et al. (2020) posted
- Wednesday after class: troubleshoot computing issues
- Friday: lab