Probabilistic Risk and Tail Risks

Lecture

Dr. James Doss-Gollin

Monday, February 2, 2026

From Climate Risk to Insurance Premiums

Target: 1:00. Open with current events that students have likely seen in the news. Don’t dive deep into insurance business—just use it as a hook.

Discussion prompts (pick 1-2 if time):

• Why would an insurance company leave a market entirely rather than raise prices?
• What happens to homeowners who can’t get private insurance?
• If “100-year floods” keep happening every few years, what does that tell us about the models?

Optional listening: NYT Daily podcast on climate insurance

Jones (2025)

The common thread: When the “worst case” keeps happening, models break down.

Today: The vocabulary and tools to talk about these tail risks.

Building on Week 2

Target: 1:02. Connect to convolution—what happens when damage function meets hazard distribution. Key point: the integral is hard, so we approximate with Monte Carlo.

\[ \begin{aligned} E[D] &= \int D(h) \cdot p(h) \, dh \\ & \approx \frac{1}{N} \sum_{i=1}^{N} D(h_i) & \textrm{if } h_i \sim p(h) \end{aligned} \]

The problem: With fat tails, this expectation is hard to estimate.

• Rare extreme events dominate the sum
• Different assumptions about tail shape → very different \(E[D]\)

Today’s Roadmap

Target: 1:04. Quick roadmap.

1. Vocabulary: Return periods and return levels
2. Fat tails: When extremes dominate
3. Risk metrics: EAD, VaR, CVaR
4. Monte Carlo: Computing any metric from samples

Vocabulary: Extreme Value Statistics

Today

1. Vocabulary: Extreme Value Statistics

2. Fat Tails

3. Risk Metrics

4. Monte Carlo for Risk Metrics

5. Wrap Up

Two Ways to Ask the Same Question

Target: 1:07. Core vocabulary slide. These two questions are inverses of each other.

Return Period (\(T\))

“How often does a flood this big happen?”

• Average time between exceedances
• \(T = 1/p\) where \(p\) is annual exceedance probability

Return Level (\(x_T\))

“How big is a T-year flood?”

• The intensity exceeded once every \(T\) years on average
• \(x_T = F^{-1}(1 - 1/T)\)

These are inverse operations on the CDF.

“100-Year Floods” and Your Mortgage

Over 30 years: \(1 - (0.99)^{30} = 26\%\) chance of at least one

• Houston experienced three “500-year” floods in three years (Harvey, Tax Day, Memorial Day)
• What are possible explanations?

Explanations include

• unlucky
• they were “500 year floods” in different dimensions and places over a big area
• climate change
• all of the above

Return Level Calculation

Target: 1:12. Show how to compute return levels from a distribution.

For a GEV distribution with parameters \((\mu, \sigma, \xi)\):

\[x_T = \mu + \frac{\sigma}{\xi}\left[\left(-\ln\left(1 - \frac{1}{T}\right)\right)^{-\xi} - 1\right]\]

In Julia, this is just:

quantile(gev_dist, 1 - 1/T)

Return Levels in Practice

Target: 1:14. Code example showing return level calculation.

# Define a GEV for storm surge (typical Gulf Coast parameters)
gev = GeneralizedExtremeValue(5.0, 1.5, 0.2)  # μ=5ft, σ=1.5ft, ξ=0.2

# Calculate return levels
return_periods = [2, 5, 10, 25, 50, 100, 250, 500]
return_levels = [quantile(gev, 1 - 1 / T) for T in return_periods]

# Plot
fig = Figure(size=(700, 400))
ax = Axis(fig[1, 1],
    xlabel="Return Period (years)",
    ylabel="Return Level (ft)",
    xscale=log10,
    title="Storm Surge Return Levels")
scatterlines!(ax, return_periods, return_levels, markersize=12)
ax.xticks = return_periods
fig

2021 Texas Freeze

Target: 1:16. Start with the concrete example. Show the graph of electricity demand vs. generation during the freeze. Point out the multi-day duration of the shortage.

Figure 1: Electricity demand (blue) exceeded supply (red) for multiple consecutive days. Source: Bryan Bartholomew on Twitter

How extreme was the cold?

Figure 2: Return period of heating demand as across space (Doss-Gollin et al., 2021).

Return Period vs. Duration

Target: 1:18. Show how the return period changes as a function of event duration. The 1-day event is relatively common, but the 5-day event is much rarer. This explains why the system wasn’t designed for it.

Figure 3: Return period of heating demand during Feb 2021 as a function of event duration (Doss-Gollin et al., 2021).

Intensity Measures Matter

Target: 1:20. Draw out the unified lesson from ERCOT. How we define the hazard determines the return period. Use consistent table format throughout.

Key insight: Return period depends on how you define the event.

ERCOT Example	Return Period	Impact
1-day cold snap	~10 years	Grid can handle
5-day cold snap	~50 years	Cascading failures

General principle: The choice of intensity measure affects everything downstream.

Hazard	Intensity Measures
Cold snaps	Peak temperature, duration, spatial extent
Floods	Depth, duration, extent, velocity
Heat waves	Peak temperature, duration, humidity

There are statistical approaches to specifying return periods for multivariate or compound extremes, such as copulas.

Fat Tails

Today

1. Vocabulary: Extreme Value Statistics

2. Fat Tails

3. Risk Metrics

4. Monte Carlo for Risk Metrics

5. Wrap Up

Normal vs. Fat-Tailed

Target: 1:22. Visual comparison is key here.

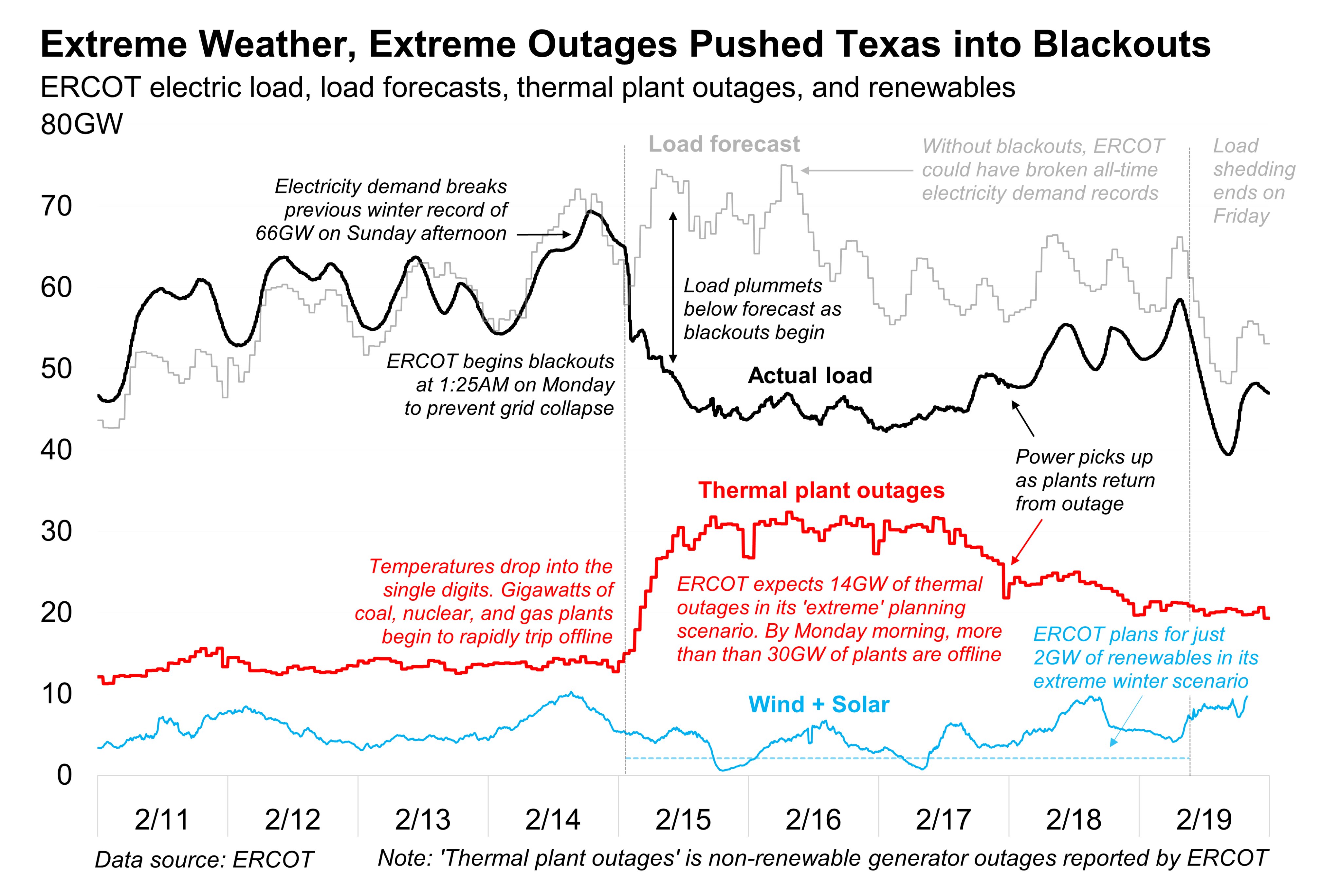
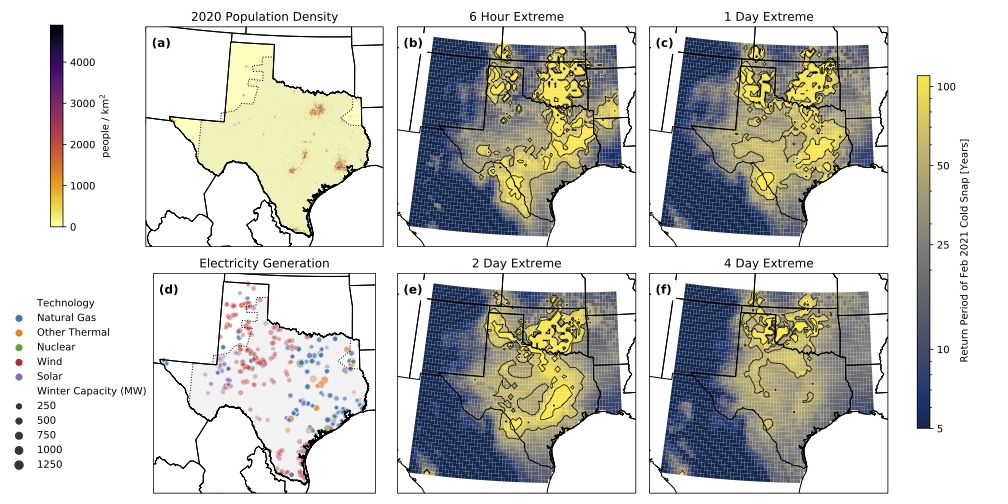
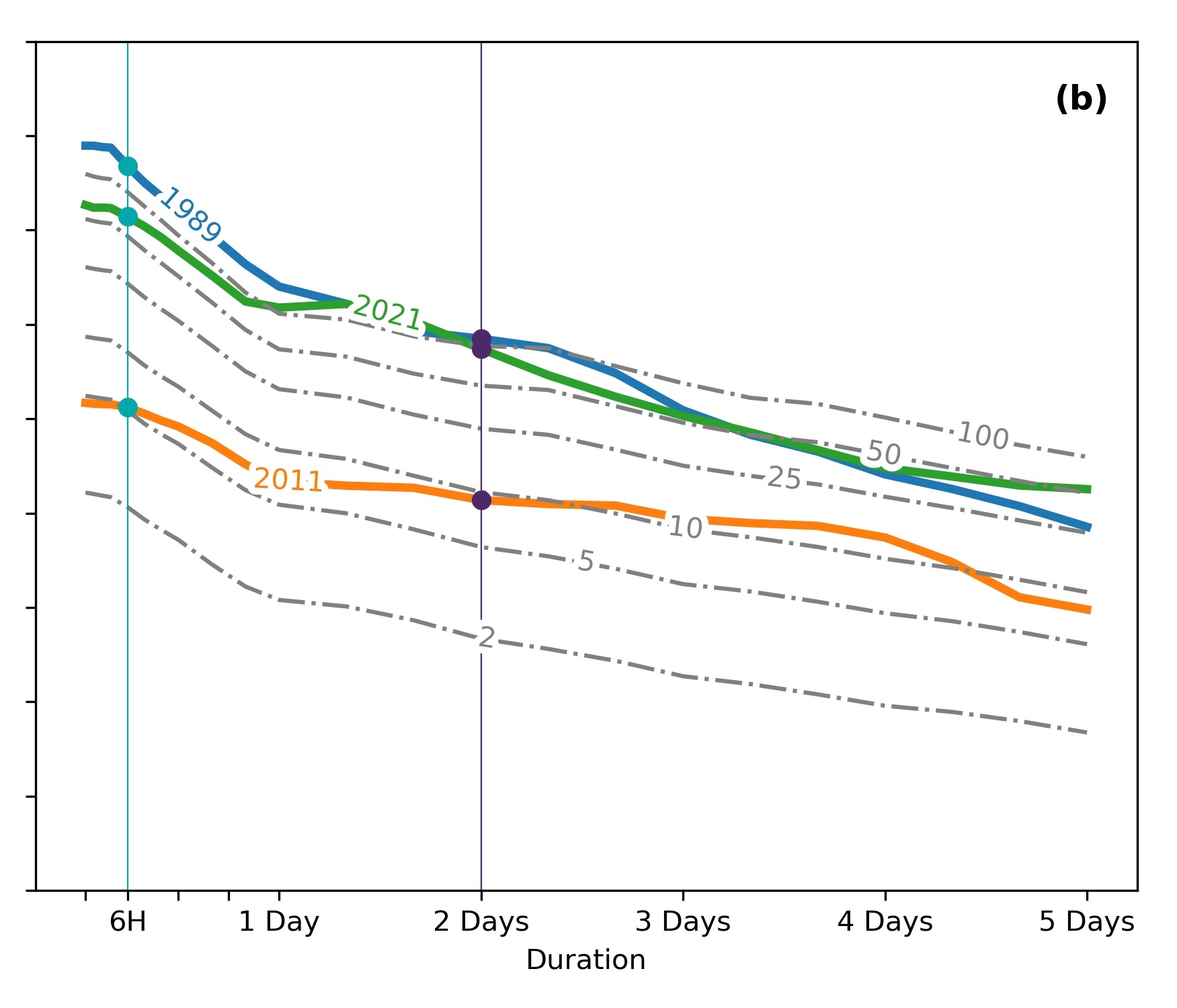
let
    fig = Figure(size=(800, 400))

    # Define distributions with different tail behavior
    # Match location/scale to make comparison "fair"
    xmin = 1.0

    # Pareto distributions with different tail indices (alpha)
    # α ≥ 2: finite mean and variance (physically plausible)
    # α ∈ [1, 2): finite mean, infinite variance (some extreme events)
    # α < 1: infinite mean and variance (very extreme, unlikely in nature)
    pareto_α2 = Pareto(2.0, xmin)  # α = 2: physically plausible
    pareto_α15 = Pareto(1.5, xmin)  # α = 1.5: very heavy tail
    pareto_α08 = Pareto(0.8, xmin)  # α = 0.8: infinite mean/variance

    # LogNormal for comparison (light-tailed relative to Pareto)
    lognormal = LogNormal(log(3), 0.8)

    # Left panel: PDFs
    ax1 = Axis(fig[1, 1], xlabel=L"x", ylabel=L"p(x)",
        title="Probability Density Functions")
    x = range(xmin, 10, length=1_000)
    lines!(ax1, x, pdf.(lognormal, x), label=L"$\text{LogNormal}$", linewidth=2, color=:blue)
    lines!(ax1, x, pdf.(pareto_α2, x), label=L"Pareto($\alpha=2$)",
        linewidth=2, linestyle=:dash, color=:orange)
    lines!(ax1, x, pdf.(pareto_α15, x), label=L"Pareto($\alpha=1.5$)",
        linewidth=2, linestyle=:dot, color=:red)
    axislegend(ax1, position=:rt)

    # Right panel: Log-scale to see tails
    ax2 = Axis(fig[1, 2], xlabel=L"x", ylabel=L"\log(p(x))",
        title="Tails on Log Scale")
    x2 = range(5, 50, length=500)
    lines!(ax2, x2, logpdf.(lognormal, x2), label=L"$\text{LogNormal}$",
        linewidth=2, color=:blue)
    lines!(ax2, x2, logpdf.(pareto_α2, x2), label=L"Pareto($\alpha=2$)",
        linewidth=2, linestyle=:dash, color=:orange)
    lines!(ax2, x2, logpdf.(pareto_α15, x2), label=L"Pareto($\alpha=1.5$)",
        linewidth=2, linestyle=:dot, color=:red)
    lines!(ax2, x2, logpdf.(pareto_α08, x2), label=L"Pareto($\alpha=0.8$)",
        linewidth=2, linestyle=:dashdot, color=:purple)
    axislegend(ax2, position=:rt)

    fig
end

Left panel shows they look similar near the center. Right panel (log scale) reveals the difference in the tails. LogNormal has exponential decay (light tail). Pareto has power-law decay - the smaller alpha, the heavier the tail.

The Pareto Tail Index

Target: 1:24. Define alpha mathematically, show estimation formula, discuss pitfalls.

For a Pareto distribution: \(P(X > x) \sim x^{-\alpha}\) as \(x \to \infty\)

Tail index \(\alpha\) controls both tail heaviness and moment existence:

\(\alpha\)	Mean	Variance	Physical Plausibility
\(\alpha \geq 2\)	Finite	Finite	Most climate/flood risks
\(1 < \alpha < 2\)	Finite	Infinite	Some extreme events
\(\alpha < 1\)	Infinite	Infinite	Unlikely in nature

Estimating the Tail Index

Target: 1:26. Show Hill estimator and its pitfalls.

Hill estimator for tail index from the \(k\) largest observations:

\[\hat{\alpha} = \left[\frac{1}{k}\sum_{i=1}^k \ln\frac{X_{(i)}}{X_{(k+1)}}\right]^{-1}\]

Pitfalls:

• Requires choosing threshold \(k\) (how many extremes to use?)
• Need many observations in the tail to estimate reliably
• Historical data often too short for rare extremes

Why Do Fat Tails Matter?

Target: 1:28. Connect to the practical implication.

For fat-tailed distributions:

• The mean can be dominated by rare extreme events
• Sample averages converge slowly to the true mean
• Historical data undersamples the tail

“The average is dominated by a small number of extreme values.”

Slow Convergence of the Mean

Target: 1:30. Adapt the running mean plot from clt.jl. Show that GEV running mean is much noisier than Normal.

let
    function running_mean(samples)
        n = length(samples)
        cumsum(samples) ./ (1:n)
    end

    n_samples = 2000
    n_lines = 8

    fig = Figure(size=(800, 400))

    # LogNormal distribution (light tail)
    ax1 = Axis(fig[1, 1], xlabel=L"n", ylabel=L"\bar{x}_n",
        title=L"LogNormal$()$: Light Tail")
    lognormal = LogNormal(log(3), 0.8)
    for _ in 1:n_lines
        samples = rand(lognormal, n_samples)
        lines!(ax1, 1:n_samples, running_mean(samples), color=(:blue, 0.4), linewidth=1)
    end
    hlines!(ax1, [mean(lognormal)], color=:black, linestyle=:dash, linewidth=2,
        label=L"\mu")
    axislegend(ax1, position=:rt)
    ylims!(ax1, 1, 6)

    # Pareto distribution (α = 1.5, fat-tailed)
    ax2 = Axis(fig[1, 2], xlabel=L"n", ylabel=L"\bar{x}_n",
        title=L"Pareto($\alpha=1.25$): Fat Tail")
    pareto_fat = Pareto(1.25, 1.0)
    for _ in 1:n_lines
        samples = rand(pareto_fat, n_samples)
        lines!(ax2, 1:n_samples, running_mean(samples), color=(:red, 0.4), linewidth=1)
    end
    hlines!(ax2, [mean(pareto_fat)], color=:black, linestyle=:dash, linewidth=2,
        label=L"\mu")
    axislegend(ax2, position=:rt)
    ylims!(ax2, 0, 15)

    fig
end

Implications for Risk Assessment

Target: 1:32. Drive home the practical point. Key insight: sample average is usually BELOW true mean for fat tails.

For fat-tailed hazards:

• Usually, the average over N years is less than the true mean
• The mean is dominated by rare extremes you probably haven’t observed yet
• Occasionally you get unlucky and observe a tail event—then your estimate jumps

Implication: Historical averages systematically underestimate risk.

We need metrics that focus specifically on the tail.

Risk Metrics

Today

1. Vocabulary: Extreme Value Statistics

2. Fat Tails

3. Risk Metrics

4. Monte Carlo for Risk Metrics

5. Wrap Up

From Expected Value to Tail Focus

Target: 1:34. Set up the progression of metrics.

Expected Annual Damage (EAD) averages over everything:

\[\text{EAD} = E[D] = \int D(h) \cdot p(h) \, dh\]

But decision-makers often care more about worst-case scenarios:

• “What’s the damage I should prepare for?”
• “What’s the catastrophic loss I might face?”

Value at Risk (VaR)

Target: 1:36. Introduce VaR with clear definition.

VaR at confidence level \(\alpha\): The \(\alpha\)-quantile of the loss distribution.

\[\text{VaR}_\alpha = F^{-1}_L(\alpha)\]

Example: 95% VaR

• “5% of the time, losses exceed this value”
• Also called: 20-year loss (same concept, different vocab)

In Julia:

VaR_95 = quantile(losses, 0.95)

VaR Illustrated

# Generate damage samples (house at 3ft elevation, $200k value)
n = 25_000
house_elevation = 3.0
house_value = 200.0  # in $1000s
hazards = rand(GeneralizedExtremeValue(5.0, 2.0, 0.1), n)
damages = [depth_damage(h - house_elevation) * house_value for h in hazards]

VaR_95 = quantile(damages, 0.95)

fig = Figure(size=(700, 400))
ax = Axis(fig[1, 1], xlabel="Damage (\$1000s)", ylabel="Probability Density", title="Damage Distribution with 95% VaR")
hist!(ax, damages, bins=50, color=(:blue, 0.6), normalization=:pdf)
vlines!(ax, [VaR_95], color=:red, linewidth=3, label="95% VaR = \$$(round(VaR_95, digits=0))k")
axislegend(ax, position=:rt)
fig

Conditional Value at Risk (CVaR)

Target: 1:42. CVaR as the solution. Also called Expected Shortfall (ES) or Tail VaR.

CVaR (Expected Shortfall): Average loss in the worst \(\alpha\)% of cases.

\[\text{CVaR}_\alpha = E[L \mid L > \text{VaR}_\alpha]\]

In Julia:

VaR_95 = quantile(losses, 0.95)
CVaR_95 = mean(losses[losses .> VaR_95])

VaR vs. CVaR Illustrated

# Compute VaR and CVaR
VaR_95 = quantile(damages, 0.95)
tail_losses = damages[damages.>=VaR_95]  # Use >= to ensure non-empty
CVaR_95 = mean(tail_losses)

fig = Figure(size=(800, 400))
ax = Axis(fig[1, 1], xlabel="Damage (\$1000s)", ylabel="Probability Density",
    title="VaR shows threshold; CVaR shows tail average")

# Main histogram
hist!(ax, damages, bins=50, color=(:blue, 0.6), normalization=:pdf)

# Add lines
vlines!(ax, [VaR_95], color=:darkred, linewidth=3, linestyle=:dash,
    label="VaR₉₅ = \$$(round(VaR_95, digits=0))k")
vlines!(ax, [CVaR_95], color=:purple, linewidth=3,
    label="CVaR₉₅ = \$$(round(CVaR_95, digits=0))k")

axislegend(ax, position=:ct, backgroundcolor=:white)
fig

Why CVaR > VaR

Target: 1:44. Use intuitive explanation, avoid jargon students don’t have background for.

VaR tells you the threshold; CVaR tells you what happens beyond it.

• VaR answers: “What loss do I exceed 5% of the time?”
• CVaR answers: “When things go bad, how bad do they get on average?”
• VaR says nothing about the severity of tail events

Example: If your 95% VaR is $100k, that just means 5% of outcomes are worse. But are they $101k worse or $1M worse? CVaR answers this.

Worked Example: Same EAD, Different Tails

Target: 1:46. Key conceptual example. Parameters chosen so hazard distributions have similar means but different tail behavior. Distribution A: Gumbel (ξ=0) with higher location Distribution B: Fréchet (ξ=0.2) with lower location to compensate for heavier tail

# Two GEV distributions calibrated to produce similar EAD but different tails
# A: Gumbel (light tail) with higher location
# B: Fréchet (fat tail) with lower location to match mean
dist_A = GeneralizedExtremeValue(5.5, 1.8, 0.0)   # Gumbel (light tail)
dist_B = GeneralizedExtremeValue(4.5, 1.5, 0.25)   # Fréchet (fat tail)

n = 50000
house_elev = 4.0
house_val = 200.0  # $1000s
damages_A = [depth_damage(h - house_elev) * house_val for h in rand(dist_A, n)]
damages_B = [depth_damage(h - house_elev) * house_val for h in rand(dist_B, n)]

# Compute metrics (use >= to ensure non-empty tail samples)
VaR95_A = quantile(damages_A, 0.95)
VaR95_B = quantile(damages_B, 0.95)
metrics = (
    EAD_A=mean(damages_A),
    EAD_B=mean(damages_B),
    VaR95_A=VaR95_A,
    VaR95_B=VaR95_B,
    CVaR95_A=mean(damages_A[damages_A.>=VaR95_A]),
    CVaR95_B=mean(damages_B[damages_B.>=VaR95_B])
)

fig = Figure(size=(800, 350))
ax1 = Axis(fig[1, 1], xlabel="Damage (\$1000s)", ylabel="Density",
    title=L"GEV($\xi = 0$) (light tail)")
ax2 = Axis(fig[1, 2], xlabel="Damage (\$1000s)", ylabel="Density",
    title=L"GEV($\xi = 0.2$) (fatter tail)")

hist!(ax1, damages_A, bins=50, color=(:blue, 0.6), normalization=:pdf)
hist!(ax2, damages_B, bins=50, color=(:red, 0.6), normalization=:pdf)

xlims!(ax1, 0, 250)
xlims!(ax2, 0, 250)
linkyaxes!(ax1, ax2)

fig

Same EAD, Different Tail Risk

Metric	Distribution A	Distribution B
EAD	$46.0k	$36.0k
95% VaR	$130.0k	$137.0k
95% CVaR	$158.0k	$174.0k

Monte Carlo for Risk Metrics

Today

1. Vocabulary: Extreme Value Statistics

2. Fat Tails

3. Risk Metrics

4. Monte Carlo for Risk Metrics

5. Wrap Up

The Monte Carlo Workflow

Target: 1:48. Review from Week 2, add emphasis on “any metric.”

1. Sample hazard scenarios from distribution
2. Apply damage function to each scenario
3. Summarize the damage samples

Once you have samples, any metric is trivial:

EAD = mean(damages)
VaR_95 = quantile(damages, 0.95)
CVaR_95 = mean(damages[damages .> VaR_95])

Computing All Metrics

Target: 1:50. Full worked example.

# Complete Monte Carlo workflow (same setup as Lab 2)
n_samples = 100_000

# 1. Sample hazards (GEV for storm surge, same as Lab 2)
surge_dist = GeneralizedExtremeValue(5.0, 2.0, 0.1)
hazards = rand(surge_dist, n_samples)

# 2. Apply damage function (house at 4ft elevation, $300k value)
base_elevation = 4.0
house_value = 300_000
damages = [depth_damage(h - base_elevation) * house_value for h in hazards]

# 3. Compute metrics
EAD = mean(damages)
VaR_95 = quantile(damages, 0.95)
VaR_99 = quantile(damages, 0.99)
CVaR_95 = mean(damages[damages.>=VaR_95])  # Use >= to ensure non-empty
CVaR_99 = mean(damages[damages.>=VaR_99])

println("Risk Metrics (house value = \$300k, base elevation = 4ft)")
println("━"^50)
println("Expected Annual Damage (EAD):     \$$(round(EAD, digits=0))")
println("95% VaR (20-year loss):           \$$(round(VaR_95, digits=0))")
println("99% VaR (100-year loss):          \$$(round(VaR_99, digits=0))")
println("95% CVaR (avg loss in worst 5%):  \$$(round(CVaR_95, digits=0))")
println("99% CVaR (avg loss in worst 1%):  \$$(round(CVaR_99, digits=0))")

Risk Metrics (house value = $300k, base elevation = 4ft)
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
Expected Annual Damage (EAD):     $67216.0
95% VaR (20-year loss):           $223965.0
99% VaR (100-year loss):          $300000.0
95% CVaR (avg loss in worst 5%):  $264827.0
99% CVaR (avg loss in worst 1%):  $300000.0

Why Monte Carlo is Essential

Target: 1:52. Connect to fat tails.

For fat-tailed distributions:

• Analytical formulas often don’t exist
• Numerical integration struggles with heavy tails
• Monte Carlo naturally captures rare events (with enough samples)

Key insight: Increase sample size when tails matter more.

Advanced Sampling (Preview)

Target: 1:54. Brief mention of advanced techniques—students should know these exist.

Naive Monte Carlo requires many samples to capture rare events:

• To get 10 samples of a 1-in-1000 event, you need ~10,000 runs

Advanced techniques can do better:

• Importance sampling: Oversample the tail, then reweight
• Stratified sampling: Ensure coverage across the distribution

These are beyond our scope, but good to know they exist when you need them.

Wrap Up

Today

1. Vocabulary: Extreme Value Statistics

2. Fat Tails

3. Risk Metrics

4. Monte Carlo for Risk Metrics

5. Wrap Up

Key Takeaways

Target: 1:56. Five bullets max.

1. Return period and return level are inverse operations on the CDF
2. Fat tails mean extremes dominate
3. We can measure fat tails using \(\alpha\) or \(\xi\)
4. EAD averages over everything; VaR gives a threshold; CVaR captures the tail
5. Monte Carlo lets us compute metrics from samples

References

Doss-Gollin, J., Farnham, D. J., Lall, U., & Modi, V. (2021). How unprecedented was the February 2021 texas cold snap? Environmental Research Letters, 16(6), 064056. https://doi.org/10.1088/1748-9326/ac0278

Jones, D. (2025). The uninsurable future: The climate threat to property insurance, and how to stop it. Yale Law Journal, 135. Retrieved from https://yalelawjournal.org/essay/the-uninsurable-future-the-climate-threat-to-property-insurance-and-how-to-stop-it